
Menu:
It seems very attractive to try and calculate the probability of completing various target scores (such as full house) from various starting positions, but in fact its appalling hard to do because there are so many combinations possible. The first roll is entirely random, but has dramatic affect on the subsequent chance of achieving a given roll, so there's no fixed starting point for an analysis. Also, the chances are affected by what has already been rolled. If you've used 5's and three of a kind already, a start throw of 5-5-3-6-4 is much less likely to yield a good result than it would at the start of a game.
The chance of rolling a yahtzee in one turn been calculated* as 4.6% or about 1 in 22 rolls but even that assumes that the player is targeting a yatzee and doesn't get tempted to go for a straight after the first roll, or take a random full house after roll two. These are things that happen in real games, so the real odds are a little less.
And this is just an analysis on one roll type, not taking into account previous scores or choices of how to select a given roll.
The attempt to statistically assess the likelihood of acheiving a given total game score is imponderably difficult .
* References - Tim Fulford Cornell University if you want to look at the derivation for yourself. In Feburary 2008 Tim went on to produce this simplest yet version of the maths.
You can try your skill playing these probabilities in an online casino.
Measured Probability of Achieving Certain Scores
In December 2007 Chris Young, a very experienced Yahtzee player, played 300 games of Yahtzee using an electronic hand held device (using the electronic device has the useful effect of gauranteeing the yahtzee rules were ruthlessly followed). The following stats were found
Number of Yahtzee's rolled = 105, or one every 2.85 games.
Low Score - 127
Highest Score with no yahtzee - 277
Highest Score with 1, 2 and 3 yahtzees - 326, 437, 504.
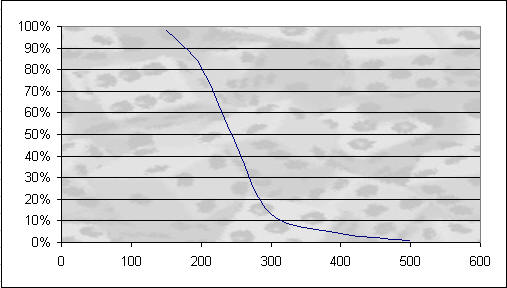
The most interesting thing to come from this trial was the probability of achieving and overall game score, shown by this table and graph
| Score At Least | Probability |
| 150 | 98% |
| 200 | 81 |
| 250 | 45% |
| 300 | 13% |
| 400 | 3% |
| 500 | 1% |
Computer
Generated Scores
In January 2008 Tim Fulford and Oliver Humpidge independantly wrote
alogrithms to simulate Yahtzee games. Oliver ran his script for 300,000
turns and found about 1:22 resulted in Yahtzee which matches theory
very closely. Tim ran his for an impressive 15 million and came up with
1:27, but his algorithm didn't seem so good at playing the game,
because it got a low score of just 37 which its doubtful if a
human player could do without deliberately aiming for a low score. Its
high score was 918. It also showed only 60% chance of scoring at least
200, compared to over 80% by human expert Chris Young. Of course its
high score is better due to the sheer number of games played.
Run
your own computer simulation
